Compute Binomial Distribution using Python from Scratch
Binomial distribution model is an important probability model that is used widely when there are two possible outcomes, for example positive reviews and negative reviews for a product rating, successes and failures in a trial. In this blog, we will compare the Binomial distribution using Python SciPy Statistical library and coding Python Statistics from scratch.
The Binomial Distribution can be expressed as
$$ P(k,n,p) = {{N}\choose{k}} \cdot p^kq^{N-k}$$From the Python SciPy Stats Library, we can get the Binomial distribution as follows:
from scipy.stats import binom
n = 50
p = 0.9
r = list(range(n + 1))
dist = binom.pmf(r, n, p)
import matplotlib.pyplot as plt
plt.bar(r, dist)
plt.show()The result is shown below
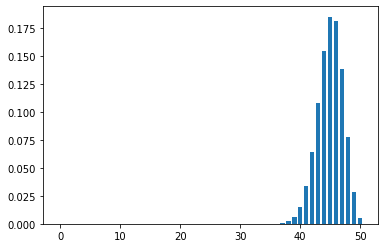
We can also code the Binomial distribution from scratch using Python as follows
def factorial(n):
x = 1
for i in range(1, n+1):
x *= i
return x
def combination(n, k):
return factorial(n)/(factorial(k)*factorial(n-k))
def binompmf(k,n,p):
return combination(n,k)*(p**k)*((1-p)**(n-k))
r = list(range(n + 1))
dist = [binompmf(k, n, p) for k in r]
import matplotlib.pyplot as plt
plt.bar(r, dist)
plt.show()The output is shown below
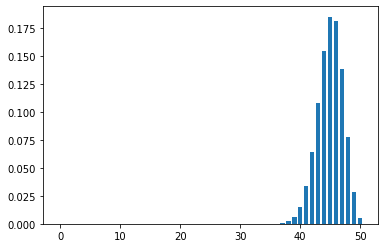
We can clearly see that both methods yield the same result
References:
Relevant Courses
August 28, 2021
